
去年底,美国数学学会(AMS)评出了2015年数学界发生的11件大事。这些关于数学和数学家的故事,无一不对数学界和一般公众有着巨大的影响,因为它们那么有趣,又被媒体铺天盖地宣传了一番。
编译沈庞
1约翰·纳什获阿贝尔奖后悲剧离世

约翰·纳什
我们要说的第一个故事是一场悲剧。就在约翰·纳什(JohnForbesNash,Jr.)于挪威首都奥斯陆(Oslo)荣获2015阿贝尔奖(AbelPrize)数天之后,他和妻子(Alicia女士)就丧生于回家的路上,双双死于发生在新泽西的一场车祸。阿贝尔奖是数学界的最高荣誉之一,2015年该奖项授予纳什和LouisNirenberg,奖励他们在非线性偏微分方程和在几何分析中的应用。纳什患有精神分裂症的艰难生活曾被改编为书和电影《美丽心灵》(ABeautifulMind),他的数学研究、生平事迹和意外逝世都被全球媒体广泛报道。
2五边形问题的新发现
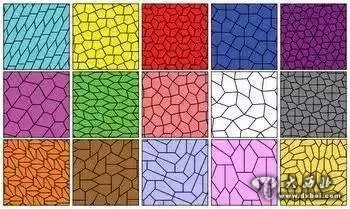
右下角就是最新发现的五边形
“设计一种五边形,用它铺满一个平面而不留下空隙,有多少种这样的五边形?”这种“平面密铺”问题一直是数学界的难题。该类问题直观地说,就是用相同的几何形状完全覆盖一个二维平面,而且图形没有重叠。密铺理论的应用颇多,比如堆放物体时,如何最大利用空间节省成本;在晶体学中,如何优化晶体结构等等。而由于正五边形的每个内角为108度,而非360度的因数,故而无法密铺平面。只能用变形的五边形挑战该问题。
“设计一种五边形,用它铺满一个平面而不留下空隙,有多少种这样的五边形?”这种“平面密铺”问题一直是数学界的难题。该类问题直观地说,就是用相同的几何形状完全覆盖一个二维平面,而且图形没有重叠。密铺理论的应用颇多,比如堆放物体时,如何最大利用空间节省成本;在晶体学中,如何优化晶体结构等等。而由于正五边形的每个内角为108度,而非360度的因数,故而无法密铺平面。只能用变形的五边形挑战该问题。
2015年,数学家终于找出了第15种五边形。参与研究的是华盛顿大学数学教授CaseyMann夫妇及学生DavidVonDerau,他们借助计算机程序成功发现了一个全新的五边形(五个角分别是60°、90°、105°、135°、150°),这也是30年来新发现的首个满足条件的五边形。正如记者AlexBellos评论:“五边形问题仍然是大多数学几何学感兴趣的领域,因为它是唯一一种尚未被完全理解的形状。”
3热门的数学教育话题

美国哈维姆德学院(HarveyMuddCollege)的TalithiaWilliams女士,她深入参与到美国STEM计划多样性研究中。STEM指科学(Science),技术(Technology),工程(Engineering),数学(Mathematics)。
数学教育一直是大家关心的热门话题。你常常能碰到对数学教学和数学学习,以及相关的社会政治问题的辩论和文章。作为常识,它能构成国家的核心标准,增加社会多样性,产生“数学素养”,甚至影响父母对子女的态度。
那么目前的数学教育面临着哪些挑战,我们又该如何改进呢?对此,媒体有大量报道,比如纽约时报曾报道的《你比8年级的孩子更聪明吗?》《新加坡奥数比赛题的病毒式传播:谢丽尔的生日是哪天》。当然还包括《数学文摘》(MathDigest)期刊的不少总结:“失败的重要性”,“旧的新数学”,“美国学生的数学能力下降”等多篇文章。
4美国队赢了国际奥数比赛

美国队成员,从左至右为:MichaelKural,YangLiu,AllenLiu,RyanAlweiss,ShyamNarayanan,andDavidStoner。
美国队以185分的总成绩“破天荒”地夺得了在泰国清迈举办的第56届国际奥林匹克数学竞赛第一名。其5名队员各获得1枚金牌,1名队员获得银牌。由于战胜了巨无霸中国队,这个消息甚至得到了白宫官方微博的祝贺。
5天才陶哲轩(TerenceTao)

1985年,陶哲轩和著名数学家保罗·埃尔德什(PaulErdős)在一起
2015年7月24日,记者GarethCook在《纽约时报》上发表了陶哲轩传记。评论家TonyPhillips称赞说:“Cook绘声绘色地描述了一个精彩的生活故事:一名澳大利亚神童在家长的适当引导下,成长为一个才华横溢、特立独行的世界级数学家。而他的报道同时又不失数学韵味,成功地让读者注意到了陶哲轩的数学工作,尤其是有关‘孪生素数猜想’和‘纳维-斯托克斯方程(Navier-Stokesequations)解的稳定性’问题。这些大体上展现了数学家的生活和他的研究…”。在宣布解决埃尔德什差异问题(ErdősDiscrepancyproblem)之后,陶哲轩再次被媒铺天盖地的报道。
6图同构问题的进展
所谓“图同构问题”(graphisomorphismproblem),即如上的二张图是否属于同构(点之间一一对应)的问题。这在复杂性理论中一直是一个特殊问题。芝加哥大学的LászlóBabai教授在去年11月的研讨会上提交有关论文,并描述了他的最新工作。他的成果旨在表明,解决这个问题只需要比多项式时间略长的拟多项式时间。大多数人都同意Babai的结果将是这个领域内的巨大进展,而且将对价值百万美元的“PvsNP问题”产生启示。不过,Babai本人并不急于宣布这点,他宁愿让同行评审先对他的成果好好核验一番。
73月14日=圆周率节
不过圆周率节(PiDay)的3月14日还有什么意思!2015年3月14日,人们按圆周率节的样子过了起来,可谓千年一遇。因为美式写法能把日期写成“3-14-15”,再加上9点26分53秒,合起来正好是3.141592653……的前几位。无论是大众社交媒体,还是各路博主,都大肆宣扬了一番。记者StevenStrogatz在《纽约时报》上发表了一段有趣的评论:“圆周率确实值得被人们变成节日来庆贺。虽然原因鲜有提及,但圆周率的美,部分源自于它使无穷的概念变得触手可及,就连小孩子也会明白。圆周率的数列不会结束,而且从未显示出规律。数列会永远地走下去,看上去是随机的,但我们又明白它不可能是随机的,因为这些数字体现了一个完美圆形里的内在秩序…”
8张益唐的数论成就
张益唐
《纽约客》杂志里很少见到为数学家写的人物传记。但也许因为张益唐被描述为“一位新罕布什尔大学的隐士般的兼职微积分教师”,所以当他在2013年提交解决那个困扰150年的未解数学难题——孪生素数猜想后,他就更让人好奇了。张益唐论证了:存在无数多对相邻素数,它们之差不超过一个固定的数值,也就并非无限(当这个距离是2时,即证明孪生素数猜想)。后来参与“博学者”项目的数学家们就在他论文的基础上,一起缩小了其中的相差。张先生因此荣获了多个奖项,他的成果发表在《数学年刊》(AnnalsofMathematics)的“素数的有界间隔”("BoundedGapsBetweenPrimes")一文中。
9JohnUrshel,一名橄榄球运动员兼数学家
image009.jpg
JohnUrschel在国家安全局发表讲话
JohnUrschel是名橄榄球运动员,同时又是个数学家!他虽然效力于巴尔的摩乌鸦队,但他也会告诉年轻人,他是多么喜欢数学。他说:“我在这个世界上最喜欢的东西都非常非常便宜,比如读数学、做研究、下棋…...我还爱上了打橄榄球。
10数学与马航MH370之谜
客机以俯仰角度-90度,渐进角度93度入水,是符合本案例的情况。该研究可在https://www.dropbox.com/s/vaf0qenjw0lk5yz/comb-90.mp4.查看,图片和视频由GoongChen等人提供。
尽管事件过去了1年多,人们还是想搞清楚一个庞大的客机是怎么从雷达上消失得无影无踪的。在数学家GoongChen的领导下,德州农工大学(TexasA&MUniversity)的7位数学家,使用计算流体力学和超级计算机的模拟,给出了MH370客机近似垂直落水的解释。这个难题随即成为一例经典的“入水问题”。该文章在2015年4月刊登在《NoticesoftheAMS》后,受到媒体关注极大关注。
112016“科学突破奖”数学奖得主IanAgol
IanAgol在加州大学伯克利分校
IanAgol是加州大学伯克利分校的数学系教授,目前在普林斯顿高等学术研究院学术休假。他获得了2016年的“科学突破奖”数学奖,表彰他在低维拓扑和几何群论领域的贡献,特别是在证明稳和问题(Tameness)、虚哈肯猜想(VirtualHakenConjecture)和虚纤维猜想(VirtualFiberingConjecture)方面的成就。“科学突破奖”由企业家扎克伯格(MarkZuckerberg)和尤里·米尔纳(YuriMilner)创立,旨在表彰优秀的科学家,就像表彰优秀演员或运动员的其他奖项一样。由于该奖奖金高达300万美元,创始人也非常著名,一向颇受媒体青睐。如同好莱坞盛会一样,它先于11月15日在美国探索频道和科学频道直播,后在11月22日由BBC世界新闻频道转播,最后福克斯电视台又在12月重播。
(责任编辑:苏玉梅)










